Usted está aquí
Materiales y recursos para enseñar y aprender líneas y puntos notables de un triángulo
Con la utilización de programas de geometría dinámica, como Geogebra, se puede estudiar este contenido matemático de una forma dinámica y divertida.
Las líneas y puntos notables de un triángulo es uno de los contenidos matemáticos que le permiten la estudiante profundizar y solucionar situaciones en contextos matemáticos y no matemáticos. Tradicionalmente ha sido enseñado con el uso de la regla y compas, que dificultaba en algunos casos la identificación y verificación de algunas propiedades por la gran utilización de trazos y marcas para su construcción. Con la utilización de programas de geometría dinámica como el Geogebra que permiten realizar ocultamientos de los trazos y movimientos de las construcciones, se facilita de visualización y verificación de las propiedades geométricas de las líneas y puntos notables de un triángulo.
Geogebra
A continuación se darán algunas orientaciones de la construcción en Geogebra de las líneas notables de un triángulo.
Para las alturas de un triángulo, se utilizan las herramientas “Polígono”, “Recta perpendicular” y “punto de intersección”. Se traza el triángulo y luego las líneas rectas que partan desde cada vértice y que sean perpendiculares a sus lados opuestos.
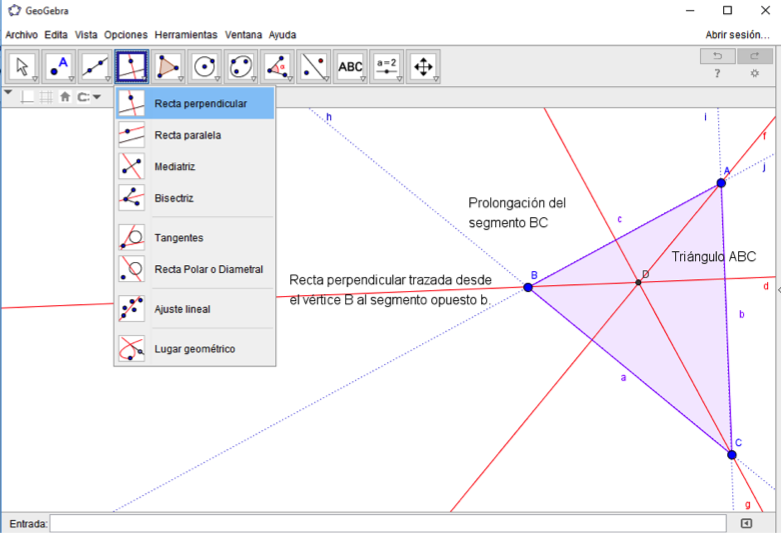
Figura 1. Alturas de un triángulo
Las herramientas a utilizar para las medianas son “Polígono”, “Punto medio” y “Segmentos”. Se traza el polígono, luego se ubican los puntos medios de los segmentos de cada lado del triángulo y se unen estos puntos mediante un segmento con sus respectivos vértices opuestos.
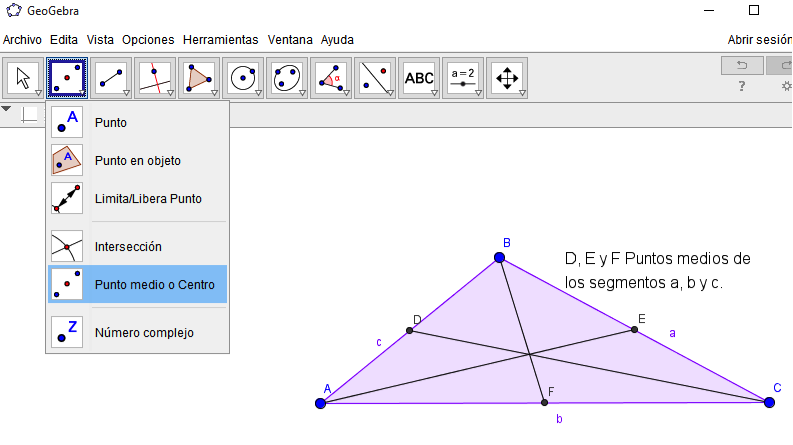
Figura 2. Medianas de un triangulo
Para trazar las bisectrices de un triángulo se explicará cómo hacerlo para un vértice, para luego seguir el mismo procedimiento para los demás vértices. Es necesario utilizar las herramientas “Polígono”, “Circunferencia (centro, punto), “Circunferencia (centro, radio), “Punto de intersección”, “Recta” y “Segmento”, así como las de “propiedades de las figuras” para diferenciar por colores y estilos de trazos las construcciones auxiliares.
Primero: Con la herramienta “Polígono”, se traza un triángulo.
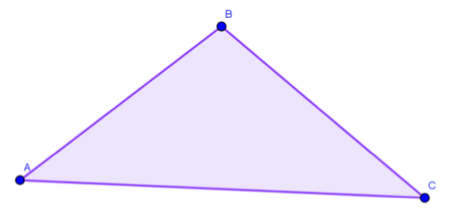
Figura 3. Triángulo
Segundo: Se traza una circunferencia con centro uno de los vértices y radio 2cm o la longitud que desee. Como el trazo de las circunferencias son construcciones auxiliares estas pueden ir con estilo de línea punteado.
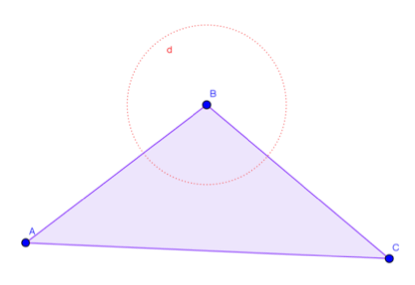
Figura 4. Circunferencia con centro en un vértice del triángulo
Tercero: Se marca los puntos de intersección entre los lados adyacentes del vértice seleccionado y la circunferencia trazada.
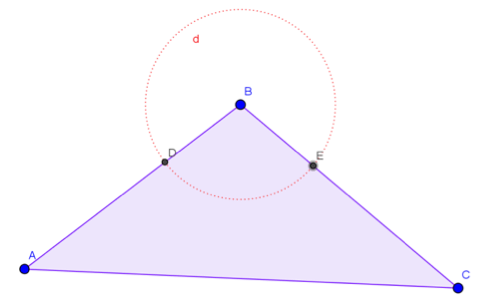
Figura 5. Puntos de intersección
Cuarto: Se trazan dos circunferencias con centro cada uno de los puntos de intersección y radio el vértice seleccionado.
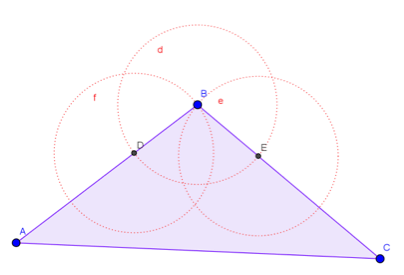
Figura 6. Circunferencias con centro en los puntos de intersección
Quinto: Se marca el punto de intersección entre las dos circunferencias trazadas.
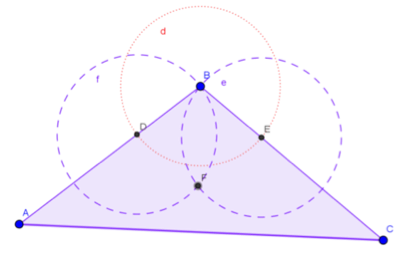
Figura 7. Punto de intersección entre dos circunferencias
Sexto: Se traza una recta que pase por el vértice seleccionado y el punto de intersección de las dos circunferencias. Se marca el punto de intersección entre la recta y el segmento opuesto al vértice.
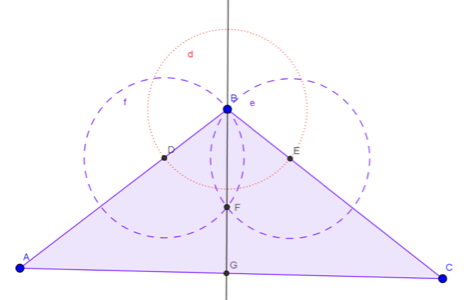
Figura 8. Recta que pasa por el vértice y el punto de intersección
Séptimo: Se oculta la línea recta y se traza un segmento que una el vértice y el punto de intersección marcado en el lado opuesto del vértice. De esta manera se obtiene la Bisectriz que divide el ángulo del triángulo en dos ángulos congruentes. Se continúa el mismo proceso con los demás vértices para obtener el incentro.
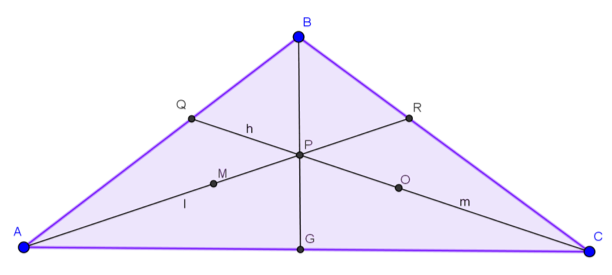
Figura 9. Bisectrices del triángulo
La mediatriz se traza con el uso de las herramientas “Polígono”, “Punto medio “, “Punto de intersección” y “Recta perpendicular”. Se traza el triángulo, luego se marca el punto medio de cada segmento y se trazan las rectas perpendiculares a los lados del triángulo que pasen por el punto medio de cada lado.
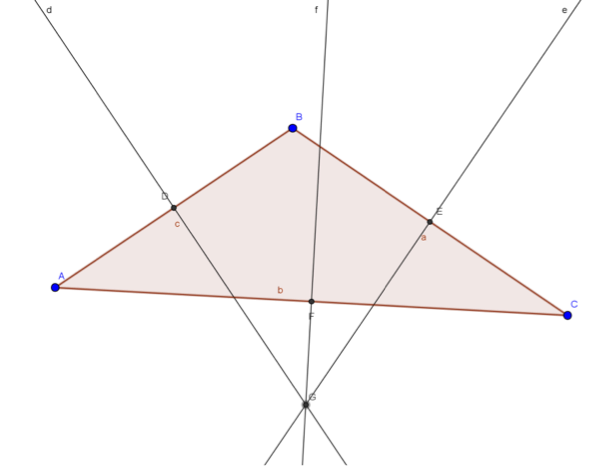
Figura 10. Mediatrices del triángulo
Con la herramienta “Circunferencia (centro, punto)” se traza la circunferencia circunscrita al triangulo ABC.
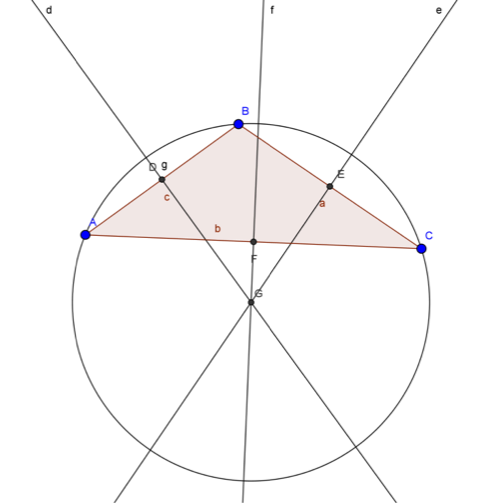
Figura 11. Circunferencia circunscrita
De esta manera se obtiene una circunferencia de centro el circuncentro y radio los vértices del triángulo ABC.
Guía para estudiantes
Guía para maestros
- 6871 lecturas







