Usted está aquí
El isomorfismo de medidas como estrategia para la resolución de problemas multiplicativos en el tercer grado de la escuela primaria
La presente investigación busca identificar las dificultades de estudiantes del segundo ciclo de primaria (8-9 años) al resolver problemas multiplicativos según la estructura del “Isomorfismo de Medidas” propuesta por Vergnaud (1995).
Introducción
La sociedad del siglo XXI en la cual vivimos, es de cambios acelerados en el campo de la ciencia y tecnología: los conocimientos, las herramientas y las maneras de hacer y comunicar la matemática evolucionan constantemente; por esta razón, tanto el aprendizaje como la enseñanza de la matemática deben estar enfocados en el desarrollo de las destrezas necesarias para que los estudiantes sean capaces de resolver problemas cotidianos, a la vez que se fortalece el pensamiento lógico y creativo. El saber matemática, además de ser satisfactorio, es extremadamente necesario para poder interactuar con fluidez y eficacia en un mundo “lleno de matemáticas”.
Es decir, los problemas y la resolución de los mismos no es sólo una actividad del matemático, sino que también es una actividad de personas o niños que aun cuando no tienen un conocimiento profundo de la matemática, realizan acciones semejantes a las del matemático, es decir resuelven problemas que la sociedad o la necesidad y su medio le presentan constantemente. En este sentido, la resolución de problemas se ha convertido en una forma de indagar los procesos del pensamiento que generan los alumnos cuando resuelven una situación problemática o problema, a la vez que permite determinar los procedimientos informales o estrategias que utilizan al enfrentarse a dichos problemas y su nivel de dificultad. Así pues, en los últimos años se ha abordado la resolución de problemas multiplicativos con el fin de elaborar una clasificación de los mismos, indagar las estrategias que utilizan los alumnos cuando los resuelven y a la vez determinar su grado de dificultad.
Antecedentes
A lo largo de la historia el estudio de las matemáticas se ha realizado desde perspectivas diferentes, a veces enfrentadas, subsidiarias de la concepción del aprendizaje en la que se apoyan. Ya en el período inicial se produjo un enfrenamiento entre los partidarios de un aprendizaje de las habilidades matemáticas elementales basado en la práctica y el ejercicio y los que defendían que era necesario aprender unos conceptos y una forma de razonar antes de pasar a la práctica y que su enseñanza, por tanto se debía centrar principalmente en la significación y en la comprensión de los conceptos.
Por tal motivo las matemáticas se han convertido en la necesidad del quehacer humano al paso de la historia y su proceso de construcción está sustentado en abstracciones sucesivas.
En la construcción de los conocimientos matemáticos, los niños también parten de experiencias concretas. Paulatinamente, y a medida que van haciendo abstracciones, pueden prescindir de los objetos físicos. El diálogo, la interacción y la confrontación de puntos de vista ayudan al aprendizaje y a la construcción de conocimientos; así, tal proceso es reforzado por la interacción con los compañeros y con el maestro. En esas actividades las matemáticas serán para el niño herramientas funcionales y flexibles que le permitirán resolver las situaciones problemáticas que se le planteen.
Así la resolución de problemas es parte fundamental y es generadora de un proceso en el cual se combinan elementos del conocimiento, reglas, técnicas, destrezas y conceptos previamente aprendidos para solucionar una nueva situación. Es así como la resolución de problemas se considera la verdadera esencia para hacer matemáticas. Algunas de las discusiones sobre las estrategias (o heurísticas) de resolución de problemas en matemática, comienzan con (Polya, 1965) que fue el primero en proponerse enseñar conscientemente el proceso de resolución de un problema. Su obra tuvo como objetivo fundamental llevar al salón de clases procedimientos, principios y recursos en general, propios del quehacer matemático. El aporte principal lo constituye el modelo planteado por él basado en las conocidas cuatro etapas: comprender el problema, elaborar un plan de solución, ejecutar el plan y análisis de la solución obtenida. En su criterio, lo más importante es lograr que el individuo aprenda a realizar conscientemente el tránsito por este camino, lo cual requiere del estudio de los métodos de solución llamados heurísticos; este es otro de sus innegables resultados. El término resolución de problemas no es privativo de la Matemática, pero la relación entre ésta y la resolución de problemas parece estar implícita tanto en las creencias populares como en determinados modelos pedagógicos.
Justificación de la Investigación
Para comprender la naturaleza de las dificultades de las matemáticas es necesario conocer cuáles son los conceptos y habilidades básicas que conlleva, cómo se adquieren y qué procesos cognitivos subyacen a su propia ejecución.
Por lo tanto el objetivo de la enseñanza de las matemáticas no es sólo que los niños aprendan las tradicionales cuatro reglas aritméticas, las unidades de medida y unas nociones geométricas, sino su principal finalidad es que puedan resolver problemas y aplicar los conceptos y habilidades matemáticas para desenvolverse en la vida cotidiana.
La orientación adoptada para la enseñanza de las matemáticas pone el mayor énfasis en la formación de habilidades para la resolución de problemas y el desarrollo del razonamiento matemático a partir de situaciones prácticas. Este enfoque implica, organizar la enseñanza en torno a seis líneas temáticas: los números, sus relaciones y las operaciones, la medición; la geometría, procesos de cambio, tratamiento de información y predicción y azar. Para lograr el aprendizaje es indispensable que los alumnos se interesen y encuentren significado y funcionalidad en el conocimiento matemático, que lo valoren y hagan de él un instrumento que les ayude a reconocer, plantear y resolver problemas presentados en diversos contextos de su interés.
Pregunta de investigación
Con el objetivo inicial de analizar cómo se presentan e interrelacionan en la enseñanza dentro del aula el planteamiento y la resolución de problemas multiplicativos con el “Isomorfismo de Medidas” y realizando el estudio de la primera fase orientado hacia la pregunta: ¿Cómo se desarrolla y relaciona el “Isomorfismo de Medidas” en la resolución de los problemas multiplicativos en el tercer grado de la escuela primaria? En particular muestro los primeros resultados de dicha fase, se lleva a cabo con treinta niños que cursan el grado señalado anteriormente dentro de un contexto escolar enmarcado en el cumplimento de objetivos y contenidos señalados por el currículo oficial.
Perspectiva teórica
La investigación se llevará a cabo con base al Modelo Teórico Local (MTL) donde el objeto de estudio se enfoca en cuatro componentes transversales, en donde sólo se abordarán dos: Modelos de Enseñanza y Modelos de Procesos Cognitivos. Para dicha investigación considero a un modelo de enseñanza como un conjunto de secuencias de textos matemáticos -porciones extensas de discurso- cuya elaboración y descodificación por el alumno le permiten dar una interpretación a aquellos textos, propuestos en un Sistema Matemático de Signos (SMS) más abstracto, y descodificarlos como mensajes con un código matemático socialmente bien establecido, es decir logra la meta educativa de dicho modelo (Filloy, 1999).
Los procesos cognitivos (Filloy, 1999) que se ponen en acción para llevar a cabo las formas del pensamiento matemático, van afinando los elementos complejos como los que se utilizan en la percepción, en el direccionamiento de la atención y sus relaciones con el proceso de comprensión, en el uso cada vez más intensivo de la memoria, el desencadenamiento de proceso de análisis y síntesis cada vez más entrelazados con el uso de la lógica, en las concepciones heurísticas utilizadas en la resolución de las situaciones problemáticas, en el aprendizaje ligado a los procesos de resolución de problemas, que requieren del uso novedoso de los SMS de la matemática escolar.
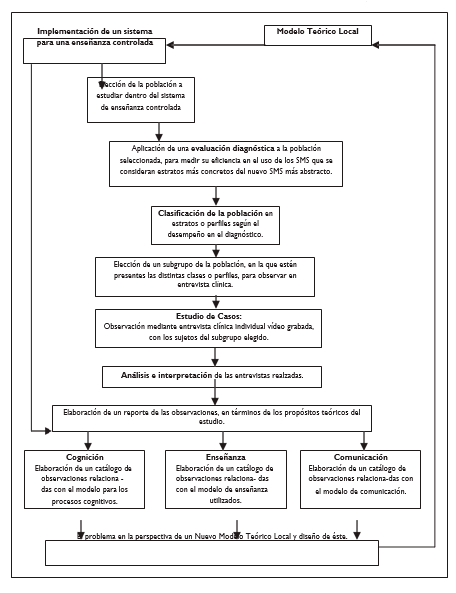
En el siguiente esquema (véase Figura 1) se muestra de manera detallada el diseño, organización y curso de la investigación.
Figura 1. Organización de la investigación y Modelo Teórico Local (MTL).
Isomorfismo
El término 'isomorfismo' significa etimológicamente 'igual forma', y con ello se quiere destacar la idea según la cual existen semejanzas y correspondencias formales entre diversos tipos de sistemas. El descubrimiento de un isomorfismo entre dos estructuras significa esencialmente que el estudio de cada una puede reducirse al de la otra, lo que nos da dos puntos de vista diferentes sobre cada cuestión y suele ser esencial en su adecuada comprensión.
En matemática la noción de isomorfismo es desarrollada en la teoría de los grupos. Esta teoría estudia los modos según los cuales cada uno de los términos de un grupo dado es sustituido, siguiendo un mismo modelo, por cada uno de los términos de otro grupo dado. Dentro de las relaciones posibles entre grupos hay la relación isomorfa. Según ella, dos grupos se llaman (simplemente) isomorfos cuando se establece una correspondencia unívoca entre los elementos de los dos grupos, y cuando el producto de dos elementos de un grupo corresponde al producto de otros dos elementos correlativos con los anteriores.
La resolución de problemas
Para trabajar la multiplicación desde el contexto de la resolución de problemas, se opta por la conceptualización propuesta por Vergnaud (1995), autor que ubica los problemas multiplicativos en el campo conceptual de la estructura multiplicativa. Vergnaud ha abordado las relaciones y operaciones y otros conceptos, creando la noción de campo conceptual: “un conjunto de problemas y situaciones para cuyo tratamiento resulta necesario utilizar conceptos procedimientos y representaciones de diferente tipo estrechamente interconectados.” (Vergnaud, 1995, p. 127)
Tradicionalmente la operación multiplicativa se ha presentado como una relación ternaria a x b = c. Para Vergnaud se trata de una relación cuaternaria entre 4 cantidades y dos tipos de medidas. Dos cantidades corresponden a medidas de un cierto tipo (por ejemplo, número de objetos) y las otras dos, son medidas de otro tipo (por ejemplo, su precio) Este análisis genera el siguiente tipo de esquema que ejemplifica los espacios de medida que se establecen y las relaciones entre las cantidades:

Isomorfismo de medidas
El Isomorfismo de medidas es una estructura que consiste en una proporción simple y directa entre dos espacios de medidas. En el “isomorfismo de medidas” con respecto a los problemas multiplicativos (Vergnaud, 1995, p. 197), se menciona que es una estructura que consiste en una proporción múltiple entre los espacios de medida: medida uno (M1) y medida dos (M2).
Considérese el siguiente problema:
“Roberto compra cuatro paletas al precio de cinco pesos cada una. ¿Cuánto debe pagar Roberto?”
En el siguiente esquema se observa el “Isomorfismo de Medidas” del problema anterior, donde M1 es el espacio de medidas (número de paletas), y M2 es el espacio de medidas el (costo de las paletas).
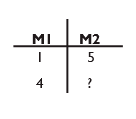
Para este autor los datos numéricos son tres: 4 paletas y una paleta que cuesta 5 pesos, entre las cuales se establece una relación de proporcionalidad directa simple.
La multiplicación puede concebirse de dos formas: como ley de composición binaria ó como una operación unitaria. En el caso de la Ley binaria el niño reconoce que debe multiplicar 4 por 5 ó 5 por 4 para solucionar el problema.
Según Vergnaud (1995), en la estructura “Isomorfismo de Medidas” se observa que:
- Se establece entre dos espacios de medida una relación cuaternaria, es decir intervienen 4 magnitudes o términos, en la cual se debe hallar el valor de una de ellas para su solución.
- El procedimiento de solución es de tipo escalar o vertical y de operador función horizontal. En el primero se establece una relación entre magnitudes del mismo espacio, mientras que en el segundo consiste en establecer una relación entre magnitudes de espacio de medida diferente.
Diseño: escenario y sujetos
La investigación se lleva a cabo en una Escuela Primaria del Distrito Federal situada en la delegación Coyoacán, se está trabajando con treinta alumnos de tercer grado de turno completo, cuyas edades oscilan entre los 8 y 9 años; se proyectó trabajar con ellos en un período máximo de cuatro semanas.
En el análisis de la dimensión curricular se examinaron los planes y programas de estudio de tercer grado de la escuela primaria, los ficheros de actividades didácticas y los libros para el maestro de los grados respectivos, así como los objetivos y contenidos que se mencionan en el eje de “los números sus relaciones y sus operaciones” y al interior de éste, el campo de los problemas multiplicativos y el algoritmo de la multiplicación. También se consultarán algunas investigaciones y libros relacionados con el tema.
El análisis continúa considerando la organización matemática propuesta en los textos escolares con respecto a los problemas multiplicativos, y para ello se analizó los libros de texto oficiales distribuidos por la Comisión de Libros de Texto Gratuitos del Gobierno Federal. En lo sucesivo se señalaron algunas coincidencias y diferencias de la organización matemática propuesta en los Planes y Programas de estudio con las propuestas en dichos libros. Una vez finalizado el análisis entre ambos se formularon hipótesis que se contrastaron empíricamente.
Para llevar a cabo esta primera fase se aplicaron ejercicios y cuestionarios exploratorios, exámenes de diagnóstico, con la finalidad de detectar las problemáticas existentes con respecto al planteamiento y resolución de problemas multiplicativos y así generar la propuesta de uso del “Isomorfismo de Medidas” -que a continuación hago referencia- para abordar estos problemas en el tercer grado de la Escuela Primaria.
Resultados preliminares
Del análisis de la propuesta institucional y del primer acercamiento empírico con los ejercicios de diagnóstico aplicados a los estudiantes resulta escaso el tratamiento de problemas multiplicativos relacionados con el Isomorfismo de Medidas, por otra parte los alumnos no dominan el algoritmo (relación ternaria) como lo señala la currícula oficial (véase Figura 2).
Figura 2.

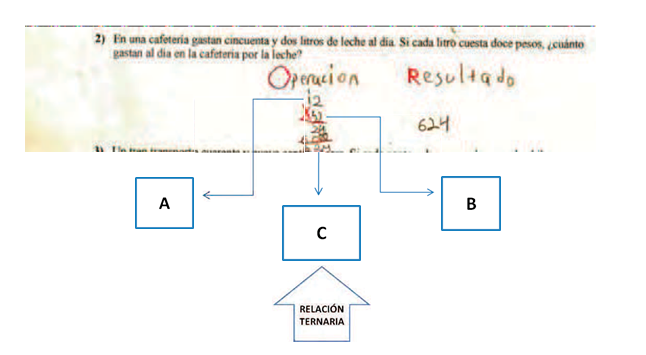
En el Plan y Programas de Estudio de la Escuela Primaria no se aborda el isomorfismo de medidas. El docente tiene escaso conocimiento sobre el “Isomorfismo de Medidas” y por consiguiente no lo aplica ni lo relaciona con el aprendizaje de sus alumnos, y sólo se centra en el uso del algoritmo con respecto a una relación ternaria (véase Figura 3) en donde al observar a los alumnos durante el desarrollo de la clase con el profesor titular la mayoría siempre preguntaba si era de suma, resta, multiplicación y división.
Figura 3.
Referencias bibliográficas
- Filloy, E. (1999). Aspectos Teóricos de Algebra Educativa. México: Iberoamérica. Polya, G. (1965). Cómo Plantear y Resolver Problemas, México; Trillas, (reimp.1996)
- Secretaría de Educación Pública, Plan y Programas de estudios 1993. Educación Básica, Primaria. México.
- Secretaría de Educación Pública, (1994). Fichero de actividades. Educación Básica Primaria. Matemáticas. Dirección General de Materiales y Métodos Educativos de la Subsecretaría de Educación Básica y Normal de la Secretaría de Educación Pública, México.
- Vergnaud, G. (l995): El niño, las matemáticas y la realidad, problema de las Matemáticas en la escuela. Trillas: México.
Escrito por: Hugo Cerritos Amador
Maestro mexicano. Cinvestav-IPN.
[email protected]
- 1099 lecturas






