El juego como medio de interacción para el aprendizaje de las matemáticas

Lizeth Katherine Medina Casallas
Universidad Distrital Francisco José de Caldas.
[email protected]   

Esta metodología se usa con el fin de hacer que los estudiantes obtengan un aprendizaje significativo de las temáticas propuestas, por medio de un proceso lúdico y dinámico; su objetivo es reflexionar acerca de los propósitos que tiene el maestro frente al proceso que enfrentan los estudiantes, sin pensar solamente en abordar muchos conocimientos para lograr todo lo propuesto por el currículo, sino que, independientemente de esto, se buscó que todo lo que se dio a conocer quedara completamente claro.

Contextualización

Esta secuencia didáctica se encuentra orientada a la innovación dentro del proceso de enseñanza, sin dejar de lado las necesidades, dificultades y/o deficiencias que tuvieron los estudiantes del grado segundo, del colegio I. T. I. Francisco José de Caldas, ubicado en la ciudad de Bogotá. El proceso llevado a cabo buscaba potenciar en los estudiantes la relación entre las operaciones básicas a través de situaciones contextualizadas, teniendo en cuenta lo propuesto en las políticas educativas.

De esta manera, la organización de este trabajo parte de las dificultades y fortalezas encontradas en el diagnóstico realizado al inicio del proceso, abordando tres campos del pensamiento matemático: numérico, geométrico y métrico, estableciendo estrechas relaciones entre estos; todo esto, con el fin de orientar la formación del estudiante a través de actividades que le permitan desarrollar un razonamiento lógico y efectivo, al igual que busque utilizar las matemáticas para interpretar y solucionar los problemas de la vida cotidiana; es indispensable que el estudiante utilice su imaginación, habilidades y destrezas para construir sus propios conocimientos, propiciando la participación activa del niño en la elaboración de dichos aprendizajes.

Así, el diseño de las actividades está basado en la teoría de situaciones didácticas propuesta desde Brousseau y fundamentadas en la resolución de problemas, ya que se convierte en un elemento transformador para el desarrollo de las clases. De esta forma, al ser vista la resolución de problemas como metodología de clase, permite el razonamiento de los estudiantes sobre cada uno de los objetos matemáticos que se están trabajando en el aula de forma dinámica, apoyados por la utilización de recursos didácticos, por medio de los cuales, es posible tener un acercamiento real a los objetos matemáticos trabajados.

Referente teórico-práctico

En el aula de clase, es común que el maestro centre más su atención en controlar el comportamiento de sus estudiantes, que en originar formas de razonamiento, que conlleven a pensar matemáticamente.

Al enseñar matemáticas no solo se abordan conceptos, métodos y procedimientos propios de esta disciplina, sino, además, una forma de pensar, hacer y comunicar; en este sentido, el quehacer matemático es una práctica que se construye y que, además, se evalúa; en términos de Vinent (2003), constantemente el ser humano está evaluando (cuando nos referimos a calidad frente a eficiencia, aciertos frente a descuidos, culpabilidad frente a inocencia, etc.) ya que siempre hay algo que evaluar.

En síntesis, es un gran reto para los maestros a la hora de evaluar, el reconocer al estudiante como persona, y no como un simple sujeto apto para aprender; sin dejar a un lado la importancia de conocer las ideas previas que poseen sobre temas que se espera trabajar, nos remitimos de nuevo a Vinent (2003) quien menciona: “El gran reto para el maestro consiste en acercarse al escolar, conocer y reconocer las características de su entorno, su manera de sentir la existencia, sus inclinaciones, sus aspiraciones, sus expectativas hacia el futuro y también sus limitaciones (...); de no ser así, la realidad de la escuela continuaría siendo ajena a la del escolar” (p. 14).

En cuanto a las políticas educativas expuestas por el Ministerio de Educación Nacional [MEN] (1998), las siguientes figuras (figura 1. Propuesta curricular para el ciclo A y figura 2. Estándares de calidad para grado segundo) exponen los aspectos relevantes para el desarrollo de este trabajo.

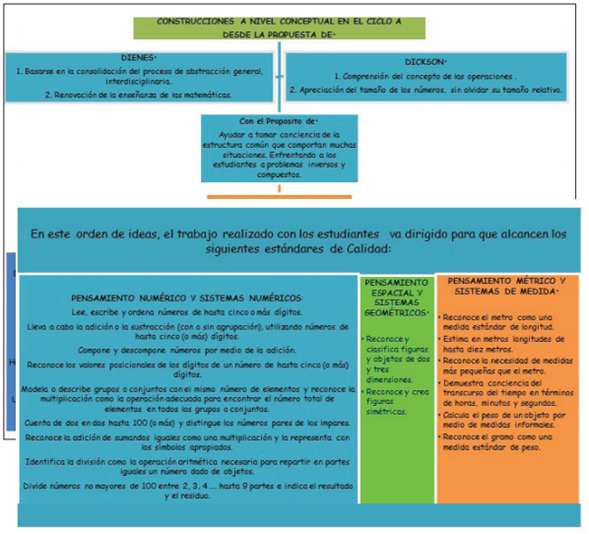
Descripción general

El proceso que se llevó a cabo parte de una situación fundamental, distribuida en diferentes situaciones a-didácticas y didácticas, donde el estudiante se involucra en un contexto, y a partir de la exploración va desarrollando habilidades que conllevan a la construcción del conocimiento, teniendo en cuenta problemáticas presentada.

Así el proceso parte de la construcción de un nuevo mundo llamado Avilandia, con ayuda de figuras de los mundos Planilandia y Solidandia, las cuales deberán contribuir en dicha construcción y la alimentación de las aves según las especies y tamaños.

De esta manera se relacionan los pensamientos geométrico (las figuras, sus componentes y propiedades), numérico (a partir de los cálculos y operaciones con los alimentos) y métrico (al determinar los patrones de medida para la construcción de las casas de las aves).

Para el desarrollo de las situaciones a-didácticas, estas se organizan en juegos, ya que es una forma más llamativa de abordar las temáticas, dichos juegos se escogieron según lo expuesto por Castaño (1995), quien menciona que en el proceso de construcción de una operación se inicia en las acciones y poco a poco se va separando de ellas, hasta llegar a representaciones cada vez más estructuradas. Así los juegos usados fueron: la cocunuba, la casa de cambio y la rana sumadora.

Mapa mental de la secuencia de actividades

Partiendo del marco de referencia plantado, se abordarán tres pensamientos matemáticos y la relación entre estos. En la figura 3 se muestra la organización de las actividades propuestas en forma de juegos y la relación con la situación fundamental.

Logros y dificultades

La situación fundamental permitió al estudiante interactuar con el medio y el profesor, a través de actividades que le posibilitaron no solo jugar sino también hacer relaciones, anticiparse a los resultados, debatir, defender sus conjeturas y adquirir un aprendizaje significativo respecto al pensamiento multiplicativo simple y complejo, valor relativo, identificación y reconocimiento de las figuras bidimensionales, secuencias y patrones, entre otros.

Así pues, el estudiante manipuló el material y relacionó cada uno de los juegos, logrando que de esta manera, que no solo se pudiera desarrollar una secuencia de actividades con un objeto matemático implícito en dichos recursos didácticos, sino que el estudiante le encontrara un significado a las actividades que estaba desarrollando con el manipulativo tangible.

En cuanto al objetivo que se trazó en este trabajo, el cual consistía en diseñar y aplicar una secuencia de actividades teniendo en cuenta la metodología de resolución de problemas para estudiantes de grado segundo, se puede decir, que más que eso se evaluó la pertinencia de cada una de esas actividades, si fueron viables o no.

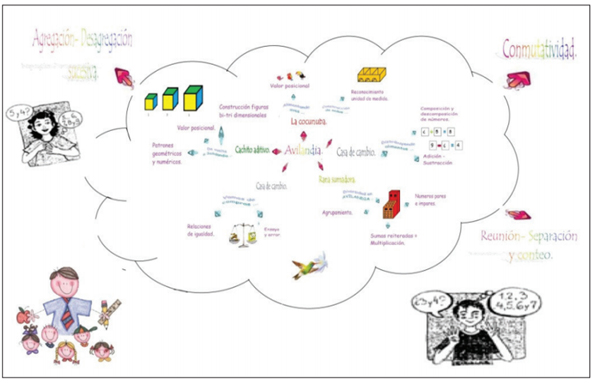
Figura 3. Mapa mental de la secuencia de actividades.

Reflexión final

El trabajo realizado en este proceso, iniciando con la planeación, el uso de recursos didácticos, la gestión del docente en el aula y la evaluación, no solo es la reunión de componentes que se enfatizaron en cada una de las prácticas docentes realizadas anteriormente, sino que, además, involucra más intensidad horaria (cinco horas semanales) y mayor interacción no solo con los estudiantes y profesores, sino también con los padres de familia, ya que la responsabilidad que se adquiere en este proceso es mayor; no solo se aborda una temática específica de un campo del pensamiento matemático sino que se deben relacionar los cinco pensamientos y todos los aspectos correspondientes a los mismos; de esta manera al tener intensidad horaria no solo se debe pensar en impartir parte del conocimiento sino que se debe poder establecer relaciones entre los saberes y los entornos de cada estudiante.

Así, el trabajo con estudiantes tan pequeños que están iniciando apenas el ciclo escolar es aún más importante, pues está en el profesor la responsabilidad de hacer del proceso enseñanza-aprendizaje algo significativo, donde los conocimientos sean los acertados y apropiados para no causarles confusiones más adelante con las temáticas a seguir; es en este ciclo donde se puede ayudar a los niños a que se motiven y encuentren el gusto por la matemática a través de las diversas situaciones o, por el contrario, se termine el gusto y sigan de alguna forma rechazando dicha área por su complejidad.

Referencia bibliográfica

• Brousseau, G. (1986). Fondements et méthodes de la didactiques des mathématiques. (J. Centeno, B. Melendo & J. Murillo).
• Castaño, J. (1995). Colección Matemática “Hojas Pedagógicas”. Serie lo Numérico. Fundación Antonio Restrepo, Ministerio de Educación Nacional. Bogotá, Colombia.
• Ministerio de Educación Nacional (2003). La revolución educativa estándares básicos de matemáticas y lenguaje, educación básica y media. Documento bajado de Internet.
• Ministerio de Educación Nacional (1998). Serie lineamientos curriculares. Documento bajado de internet.
• Vinent, M. (2003) Trazas y miradas. Evaluación y competencias. Una mirada a la evaluación. Documento bajado de Internet. Recuperado en octubre 18 de 2011 de: http://www.bdigital.unal.edu.co/1559/2/01PREL01.pdf