Lectura crítica y lógica filosófica o ¿Cómo leer el “entrelíneas” de un texto filosófico y uno no filosófico?

Nivel: Décimo
Área: Ciencias Sociales, Filosofía
Institución: Institución Educativa Compartir Suba

Si se quiere sensibilizar al estudiante sobre la importancia de hacerle preguntas a un texto desde las herramientas de la lógica (simbólica, de clases, proposicional) debemos preguntarnos

I) ¿Cómo integrar el cálculo lógico a la lectura de textos filosóficos y no filosóficos?

II) ¿Cómo hacer atractiva y productiva tal empresa?

Así, basta con bibliografía base como el  “El elogio de la dificultad” y “Sobre la lectura” de Estanislao Zuleta; un libro de texto escolar de filosofía con temáticas de lógica; conocimientos básicos en gramática y matemáticas; y, un poco de la jerga cotidiana del estudiante al que nos dirigimos.

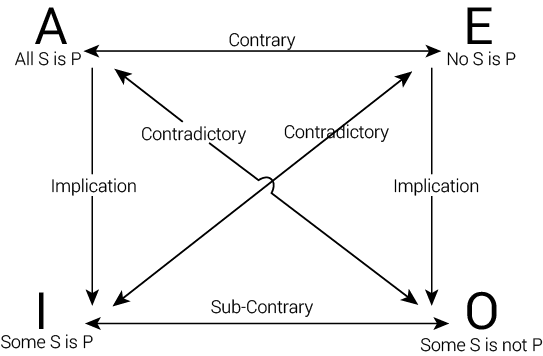
Sin más exponemos, a través de pequeñas frases del argot juvenil, los conectores lógicos y las maneras en las que se usan, además de los cuantificadores y la constitución de la proposición. A la hora de hacer esta traducción a lenguaje lógico cada concepto del texto será un sujeto o un predicado que se relacionan como si de lógica de conjuntos se tratase. En el tablero podemos tener estos gráficos a la mano: conectores lógicos, cuantificadores y tipos de proposiciones en el cuadro de oposición de Aristóteles¹.

De tal modo, la frase “Si lo pego no está mal” podría traducirse como dos proposiciones simples (una con cópula afirmativa y otra con negativa) conectadas a través de un condicional. Algunos estudiantes suelen creer que sólo hay una idea cuando realmente habría dos. Ellos olvidan, o no se percatan, que hay un sujeto y está implícito, que se predica uno cosa de él y otra de su actuar. ¿Quién pega y qué pega? ¿Qué se dice de tal acción?

La traducción sería: Y es P[x] → P[x] ∼es M, donde Y es equivalente a YO, P a PEGAR, [x] a LO QUE SE PEGA, y M a MAL; la cópula – el verbo “estar” en tercera persona, que es como se maneja en la lógica aristotélica – está en singular en las dos proposiciones, pero afirmado en la primera (es) y negado en la segunda (∼ es). Y, se leería así: “Si yo lo pego, entonces esto no está mal”, donde podemos ver como al traducir a lenguaje lógico cada concepto del texto será un sujeto o un predicado que se relacionan como si de lógica de conjuntos se tratase a través de la cópula.

Si queremos usar los cuantificadores, en vez de escribir “Y” reemplazamos por “Ǝx”, con lo cual tendremos que: “Ǝx es P[x] → P[x] ∼es M”. Para el trabajo en inglés, el verbo “to Be” cuenta con la ventaja de cumplir la función de “ser” y “estar”; así, con el mismo ejemplo, “I is P[x] → P[x] ∼is B”, teniendo: “I”, “Paste”, “Bad” and “is”; se leería así: “If I am pasting it, then it is not bad”.

Después de que cada estudiante se relacione mejor con las herramientas lógicas mediante trabajo en grupos (parejas o cuartetos) en los que leerán y traducirán a términos lógicos un texto filosófico como los de Estanislao Zuleta ya mencionados, cada uno socializa al resto de la clase la forma en que tradujo una frase y es corregido por la clase en pleno. Ahora, y para evaluar de otro modo el aprendizaje, los estudiantes se enfrentarán con textos no filosóficos, ya no de su argot juvenil, sino de la cosecha del día a día, a los que aplicarán la herramienta descrita. Por ejemplo, con la respuesta de una reina de belleza ya famosa, Verónica Velásquez, Ex Señorita Antioquia 2010:

“Yo creo que el hombre se complementa al hombre. Mujer con mujer, hombre con hombre, y también mujer a hombre, del mismo modo en el sentido contrario…”

Su traducción a términos lógicos, usando conectores, cópulas, nominación tipo conjunto – es decir tomando la(s) primera(s) letra(s) del concepto en juego; si es “Creo”: “Cr”, por ejemplo –,genitivos (los paréntesis usados en las funciones como f (x), que muestran una relación; así “complemento del hombre”: “Co (H)”) –, además de corchetes para aclarar información: ¿Qué es lo que se cree? Se cree que el hombre complementa al hombre: “Cr [ H es Co(H) ]”  –, bien podría ser:

Y es Cr [ H es Co(H) ] ∧ Y es Cr [ M es Co(M) ∧ H es Co(H) ∧ M es Co(H) ↔ Co es Mo [m] ∧ S [con] ]

Finalmente, el estudiante reflexionará si su nivel de lectura es el mismo, si alcanzó o no una mejor comprensión y, si el hacer esas traducciones le permiten crear hipótesis sobre qué dice el texto y por qué. Así, se ha hecho de un texto aparentemente fácil, uno complejo. Hemos visto la importancia de la filosofía, su hacer preguntas y su rigurosidad a través de la lógica, en la lectura crítica de un texto: hemos leído e ido más allá.

Es satisfactorio ver cómo durante el proceso el estudiante se apasiona por el grado de dificultad que le implica este tipo de trabajo con un texto, además, cómo algunos de ellos terminan viendo como en una respuesta de reina, es decir una en donde se improvisa algo medianamente coherente bajo la presión del nerviosismo, se esconde toda una construcción lógica que permite preguntarse qué quería decir ella y cómo interpretarla sin caer en juzgarla a la ligera, en una lectura poco o nada crítica, sino llena de prejuicios, cerrada.

Guía para el maestro