Adición de fracciones, materiales y recursos

Es necesario aprender a operar las fracciones utilizando diferentes estrategias que permitan comprender el proceso realizado. A continuación se describe el uso de las transparencias de fracciones para la operación de adición.

Transparencia de fracciones

Las transparencias de fracciones son dos hojas, una en cartulina y otra en acetato. Con cuadrados de igual tamaño divididos en partes iguales de . Con este material se puede representar fracciones, realizar comparaciones, operaciones de adición, sustracción, multiplicación y división.

Para adicionar las fracciones 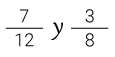procedemos de la siguiente manera. Iniciamos representando las fracciones como se muestra en las figuras 2 y 3

Figura 2. Representación 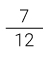 de  en la cartulina

Figura 3. Representación de 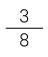 en el acetato.

Luego ubicamos el acetato en forma perpendicular a la cartulina, de tal manera que se obtiene lo siguiente. (Figura 4)

Figura 4. Representación de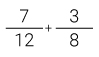

Por último, las partes azules que quedaron sobre las rosadas las ubicamos en la región que quedo sin colorear. Para hallar la suma de las dos fracciones simplemente escribimos la fracción que relaciona el total de partes coloreadas con el total de divisiones del cuadrado.

Figura 5. Representación de la suma de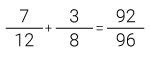 

Otro recurso que se puede emplear es la calculadora de fracciones, que encontramos disponible en internet. Con solo ingresar las dos fracciones o números mixtos y el signo de la operación a realizar, la aplicación muestra el paso a paso del procedimiento realizado. Permitiendo que el estudiante identifique la conversión de números mixtos a fracción, el común denominador y las fracciones equivalentes a las dadas inicialmente.

Referencias

• Calculadora de fracciones disponible en http://es.onlinemschool.com/math/assistance
• Segovia, I. Rico, L. (2011). Matemáticas para maestros de Educación Primaria. Capítulo 8. Números Racionales. Flores, P. Torralbo, M. Editorial Pirámide. Madrid

Guía para los maestros

Guía para los estudiantes