Expresiones algebraicas, materiales y recursos

En la enseñanza de las matemáticas el lenguaje algebraico es utilizado para generalizar operaciones aritméticas, resolver problemas mediante ecuaciones, representación de funciones y como símbolos abstractos.

Agosto 11, 2015

Las traducciones entre el lenguaje cotidiano y el matemático requieren del estudiante, la comprensión del significado y uso de los símbolos y letras dentro de una expresión. De ahí que es necesaria la utilización de material concreto en el proceso de enseñanza de las expresiones algebraicas para lograr que el estudiante determine el significado matemático de las letras y signos en una expresión.

Tableros de fichas de colores

Es un material compuesto por un tablero en forma de rectángulo dividido en dos cuadrados, que puede ser construido en cartulina, y fichas de dos colores y formas cualesquiera. Como ejemplo se utilizaran fichas de color amarillo para representar incógnitas y valores positivos, los negativos con color violeta. Las formas de círculo, triangulo, rombo, pirámide, cuadrado, rectángulo y cubo, aunque se pueden agregar otras formas para representar más incógnitas. La tabla 1, muestra la representación y equivalencia de cada forma.

Tabla 1. Representación y equivalencia de cada forma

Para jugar se ubican las fichas en el tablero y se representa simbólicamente el significado de las mismas como se muestra en la figura 1. Por ejemplo “el triple de un número aumentado en dos es 9”

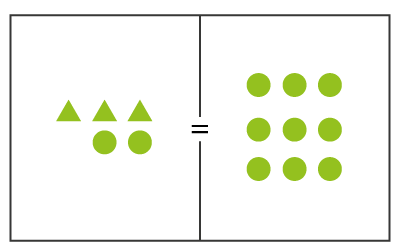
Figura 1. Ubicación de las fichas de la expresión

De esta manera queda representada pictóricamente la expresión, luego el estudiante debe deducir la expresión algebraica . Ahora si lo que se pretende es que el estudiante encuentre el valor numérico de la variable (incógnita), la regla principal es que parejas de la misma forma pero de distinto color en un mismo lado del tablero se eliminan. Así el juego consistiría en aislar las fichas de los triángulos que representan las incógnitas en un solo lado del tablero.

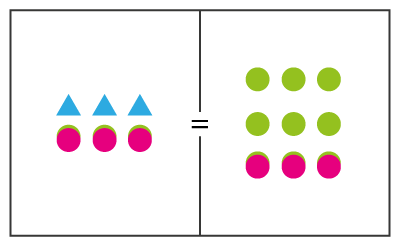
Figura 2. Sustracción de tres unidades enteras

De esta manera se obtiene (tres triángulos y 6 círculos), puesto que la operación inversa de la multiplicación es la división, entonces, se divide los seis círculos en tres grupos, dos por cada triángulo, obteniendo lo siguiente.

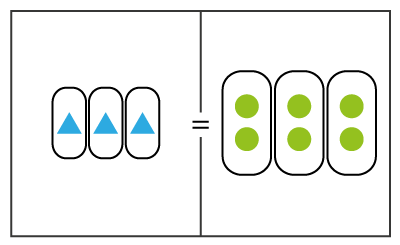
Figura 3. Agrupación de círculos en tres grupos

De ahí que la respuesta final es , como lo muestra la figura 4.

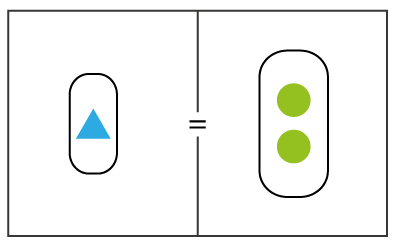
Figura 4. Representación del valor numérico de la incógnita

Como se observa en las figuras, además de representar una expresión del lenguaje cotidiano en el lenguaje pictórico y algebraico, con el uso del material también se puede encontrar el valor de las incógnitas cuando estas representan expresiones lineales.