Usted está aquí
Sucesiones con el juego las torres de Hanói
Las torres de Hanói son un excelente recurso en el aula para introducir a los escolares en la búsqueda de patrones y regularidades; en otro sentido, permite al docente introducir, en el aula, temáticas relacionadas con sucesiones numéricas.
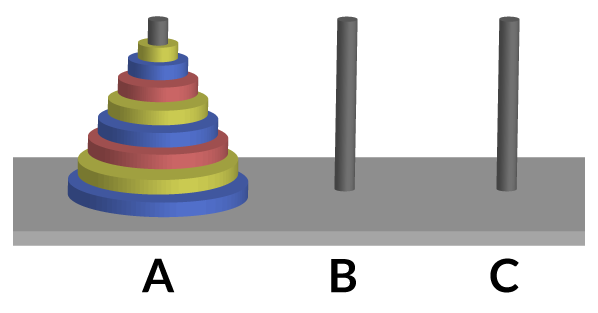
La “Torres de Hanói” es un juego matemático inventado en 1883 por el matemático francés Éduard Lucas. Basicamente, consiste en tres varas verticales puestas en una misma base. En la primera de ellas se ubican discos de diferente tamaño y el objetivo consiste en trasladar los discos de la primera vara hacia la tercera vara.
A mayor cantidad de discos, mayor será la complejidad de la solución. Desde la base, los discos se apilan de mayor a menor. Para completar el juego, es necesario seguir tres simples reglas:
- Sólo se puede mover un disco cada vez.
- Un disco de mayor tamaño no puede descansar sobre uno más pequeño
- Sólo se puede desplazar el disco que se encuentre arriba en cada varilla.
La estrategia es encontrar la menor cantidad de pasos para cumplir con el objetivo. Si se observa, la cantidad de pasos para solucionar una torre de Hannoi dependera de la cantidad de discos. La siguiente regularidad muestra la relación.
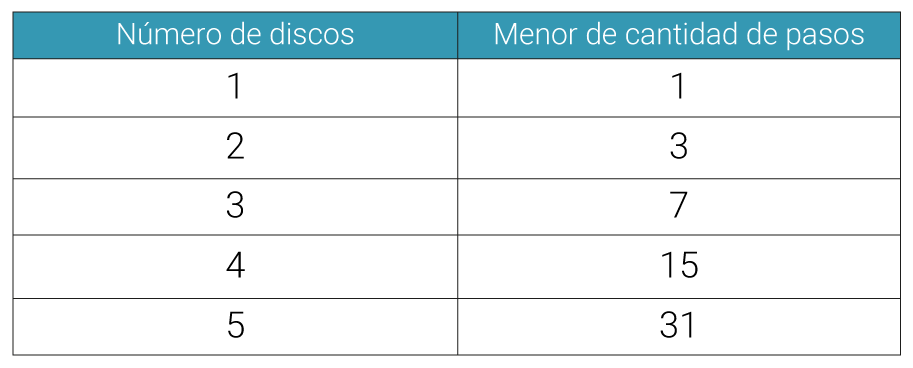
Es decir, que para seis discos la cantidad de pasos correspondientes sería 63. Una estrategia para lograr predecir el número de pasos a partir de la cantidad de discos es sumar una unidad a todas los valores de la cantidad de pasos. De esta manera, resultan los números 2, 4, 8, 16, 32 y 64, conjunto equivalente a las potencias de base dos. Es decir, el número de pasos es equivalente a dos elevado a la cantidad de número de discos reducido en una unidad. Si n es la cantidad de discos, entonces la menor cantidad de pasos será:
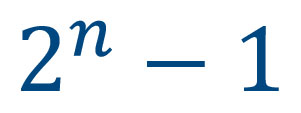
El acceso de los escolares al material en físico en algunos casos puede ser una limitante. Aunque ello, se solucionaría con recursos digitales en la web que simulan el juego www.disfrutalasmatematicas.com.
Guía para los maestros
Guía para los estudiantes
- 13195 lecturas







