Muro de fracciones

Como solución,  pretenderé exponer  una alternativa de trabajo con  un material  conocido como el muro de fracciones, optando por facilitar esos procesos de comprensión y aprendizaje de las fracciones en los estudiantes. En el siguiente texto, encontraras una guía que te explicará paso a paso las recomendaciones generales para llevar a cabo una sesión de clase con el muro de fracciones. Posteriormente, una guía para el estudiante, cuyo propósito es ser instrumento de trabajo por parte del escolar, y por último, expondré el material necesario para desarrollar la sesión.

El muro de fracciones o también conocido el diagrama de Freudenthal es un material  que permite la conceptualización de la fracción, establecer relaciones entre estas y desarrollar ciertas operaciones.

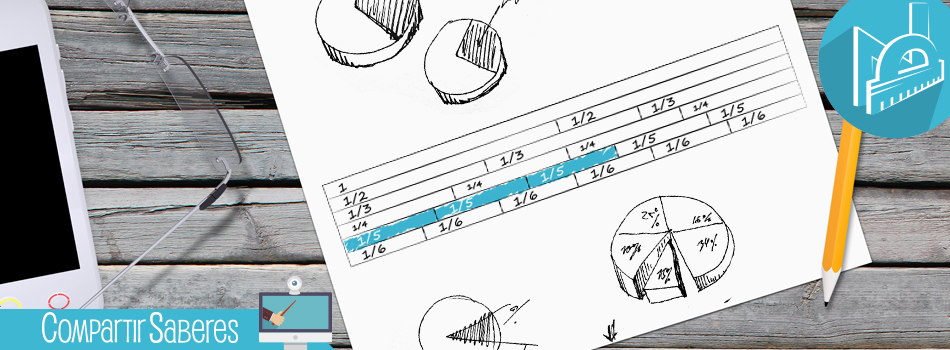
El muro de fracciones es un diagrama rectangular dividido por franjas horizontales, donde cada una de éstas agrupa familias de fracciones unitarias. En la parte superior de representa la unidad (el número uno).  La segunda franja se divide en dos, cada una de las divisiones representa un medio. La tercera en tres y cada una representa un tercio y así sucesivamente.

Para desarrollar una sesión de clase, cuyo objetivo principal es lograr que el estudiante comprenda las nociones básicas de una fracción utilizando el muro de fracciones, puedes estructurar la clase en los siguientes momentos:

• Presentación del muro de fracciones
• Creación de un lenguaje para Identificar las partes del muro de fracciones
• Definir la unidad
• Saber cómo utilizar el muro de fracciones
• Retar a los estudiantes con problemas de fracciones en el muro de fracciones
• Proponer problemas de relaciones de fracciones con el muro de fracciones

Con estos momentos se pretende que el estudiante reconozca el sentido básico de la fracción como una relación parte-todo.

Presentación del muro de fracciones

Lo ideal es que cada niño tenga en sus manos el muro de fracciones. El estudiante tendrá mucho más manejo y cercanía con el material. Es indispensable, cuestionar al estudiante sobre las características propias de la materia. Por ejemplo, ¿Cómo son las formas del muro de fracciones? ¿Qué ocurre con los trazos de arriba a abajo?

Creación de un lenguaje para Identificar las partes del muro de fracciones

Es indispensable, brindarle al estudiante instrucciones básicas sobre las partes del muro de fracciones. Con ello el manejo y la descripción de procesos en el muro serían muy fácil. Por cuestiones metódicas, cada franja o  división horizontal del muro puede llamarse como nivel o bloque, mientras que cada división en  éstos, puede llamarse ladrillo.

Definir la unidad

Definir la unidad no es algo sencillo, más aún, si los estudiantes pertenecen a un grado menor de escolaridad. Por tal motivo,  es recomendable asociar la unidad a palabras como un  “todo” o simplemente el correspondiente al número 1. En el caso del muro de las fracciones, corresponderá al nivel o bloque ubicado en la parte superior. Es decir, el bloque que está compuesto de un solo ladrillo o el cual no contiene división.

Saber cómo utilizar el muro de fracciones

Conocidas las partes e identificada la unidad, se puede dar claridad sobre el uso del muro de fracciones. Se puede pedir a los estudiantes colorear cada bloque de un color distinto. Por tal razón, los ladrillos de un bloque se reconocerían porque todos llevan el mismo color.  Además, podría pedírsele a los estudiantes plastificar el muro, lo que permitiría rayarlo con marcadores borrables.

Cada bloque del muro representa una familia de fracciones propias (menor que la unidad). El segundo bloque o franja representa los medios, pues la unidad se divide en dos. El tercero los tercios, el cuarto los cuartos, y así sucesivamente. La descripción de las particiones puede llegar hasta donde finalice el último bloque del muro.

Se puede decir que uno o varios ladrillos de un muro corresponden una fracción. Para dar a entender esto, también se podría dar a los estudiantes fracciones propias con lo que los estudiantes tendrían que explorar la manera de hallar las fracciones en el muro o colorearlas. Por ejemplo, tres ladrillos del bloque de los quintos representaría tres quintos (3/5). Sería adecuado, exponer varios ejemplos de ubicación de fracciones muro dada la fracción o viceversa. Si se desea facilidad en la manipulación del muro, se puede pedir a los estudiantes ubicar una regla de manera vertical al lado derecho de la fracción representada por los ladrillos de un bloque.

En el ejemplo de la figura anterior se representa sombreada de azul la fracción tres quintos (3/5)

Retar a los estudiantes con problemas de fracciones en el muro de fracciones

En este caso, se pretende que los estudiantes manejen de manera autónoma en la utilización del muro de fracciones. Se puede pedir resolver situaciones donde se deba reconocer una fracción en el muro. Otro caso, identificar relaciones existentes entre  fracciones en el muro. Por ejemplo ¿Qué fracción es la mitad de ½? ¿Cuáles fracciones ocupan el mismo espacio en un bloque al igual de ½? ¿Qué fracciones ocupan más espacio o menor espacio en un bloque que 2/5? Ello daría, no sólo a la conceptualización de la fracción, sino al reconocimiento de relaciones existentes como la equivalencia y el orden.

Como extensión,  se pueden agrupar a los estudiantes con el fin de resolver situaciones que impliquen una extensión de las fracción menores que la unidad. Por ejemplo. Si desean ubicar 5/3 en el muro, tendrán que ubicar dos muros a lados y lado de tal manera que el bloque de los tercios este junto al otro. Con ello, identificarían que cinco tercios son un bloque completo de los tercios más otros dos ladrillos de los tercios.

La potencialidad del uso del muro de fracciones no se limita al reconocimiento de características y de las relaciones de la fracción. Pueden incluirse situaciones asociadas a la suma resta de fracciones, lo que llevaría al desarrollo de otras sesiones de clases.

La utilización del muro de fracciones tiene muchas ventajas, pues las instrucciones son mínimas y fáciles de comprender. No se requieren muchos conocimientos previos, por lo que es una excelente herramienta para conceptualizar o profundizar el tema de fracciones en cualquier nivel de escolaridad. Una desventaja es que no todas las fracciones pueden representarse (tal como ocurre con grandes fracciones o  con denominador grande) y el desarrollo de operaciones complejas es complejo y engorroso.

La guía de estudiante  encontrara 5 ítems para desarrollar durante la sesión; El muro de fracciones podrá ser copiado para el trabajo en la sesión de clase. Al cierre de la guía del estudiante, el estudiante encontrara una serie de criterios de autoevaluación  con el fin de observar el alcance de proximidad que adquirió el escolar en la experiencia del desarrollo de la misma. 

Referencias

Flores, P., Lupiáñez, J. L., Berenguer, L., Marín, A. y Molina, M. (2011). Materiales y recursos en el aula de matemáticas. Universidad de Granada. Departamento de Didáctica de la Matemática. digibug.ugr.es/bitstream/10481/21964/1/libro_MATREC_2011.pdf

Guía para el Maestro

Guía para el estuduante